Bayesian Basics
Wherein I apply Bayes’ Theorem to something we’re all thinking about.
$$P( A | B ) = \frac{P( B | A) P(A)}{P(B)}$$
It looks simple, but Bayes’ Theorem is a little un-intuitive, at least when I first came across it. I kept reading blog posts and the Wikipedia entry and math papers and finding descriptions like this:
$$\underbrace{P( A | B )}_{\textsf{posterior}} = \underbrace{\frac{P( B | A) }{P(B)} }_{\textsf{support}} \underbrace{P(A)}_{\textsf{prior}}$$
or this:
$$\underbrace{P( A | B )}_{\textsf{posterior}} = \frac{\overbrace{P( B | A) }^{\textsf{likelihood}} ~ \overbrace{P(A)}^{\textsf{prior}}}{\underbrace{P(B)}_{\textsf{marginal probability}}}$$
which certainly defines terminology, and even provides some intuition for how to understand the terms, but it doesn’t really tell you what to do.
I finally figured out that, as Bertrand Russell put it in The Problems of Philosophy,
The fact is that, in simple mathematical judgements such as 'two and two are four', and also in many judgements of logic, we can know the general proposition without inferring it from instances, although some instance is usually necessary to make clear to us what the general proposition means. This is why there is real utility in the process of deduction, which goes from the general to the general, or from the general to the particular, as well as in the process of induction, which goes from the particular to the particular, or from the particular to the general.
In this case, it means puzzling through a basic probability problem based on Bayes’ Theorem. So, to choose a problem that we’re living through as of writing (Feb 2021), let’s ask:
What is the probability that I have Disease X given a positive test from a test kit?
In the math equation above, this would read $P(\textsf{Disease X} | \textsf{pos. test})$, and therefore that
$$P( \textsf{Disease X} | \textsf{pos. test} ) = \frac{P( \textsf{pos. test} | \textsf{Disease X}) ~ P(\textsf{Disease X})}{P(\textsf{pos. test})} $$
So we need three bits of information here: the probability that we get a positive test given the presence of Disease X (the true positive rate of the test), the probability that I’d have Disease X (i.e. its prevalence in the population), and the probability that I would get a positive result on the test (the true positive plus false negative rate of the test).
What’s the Diagnosis?
Let’s say the disease has a 1% prevalence in the population, meaning that at any given time 1% of the population has the disease. Let’s say our test was developed in haste, and has a 30% false positive rate. Let’s also say that we decided we accepted this high rate of false positives to have very few false negatives, so we only have maybe a 1% rate of false negatives.
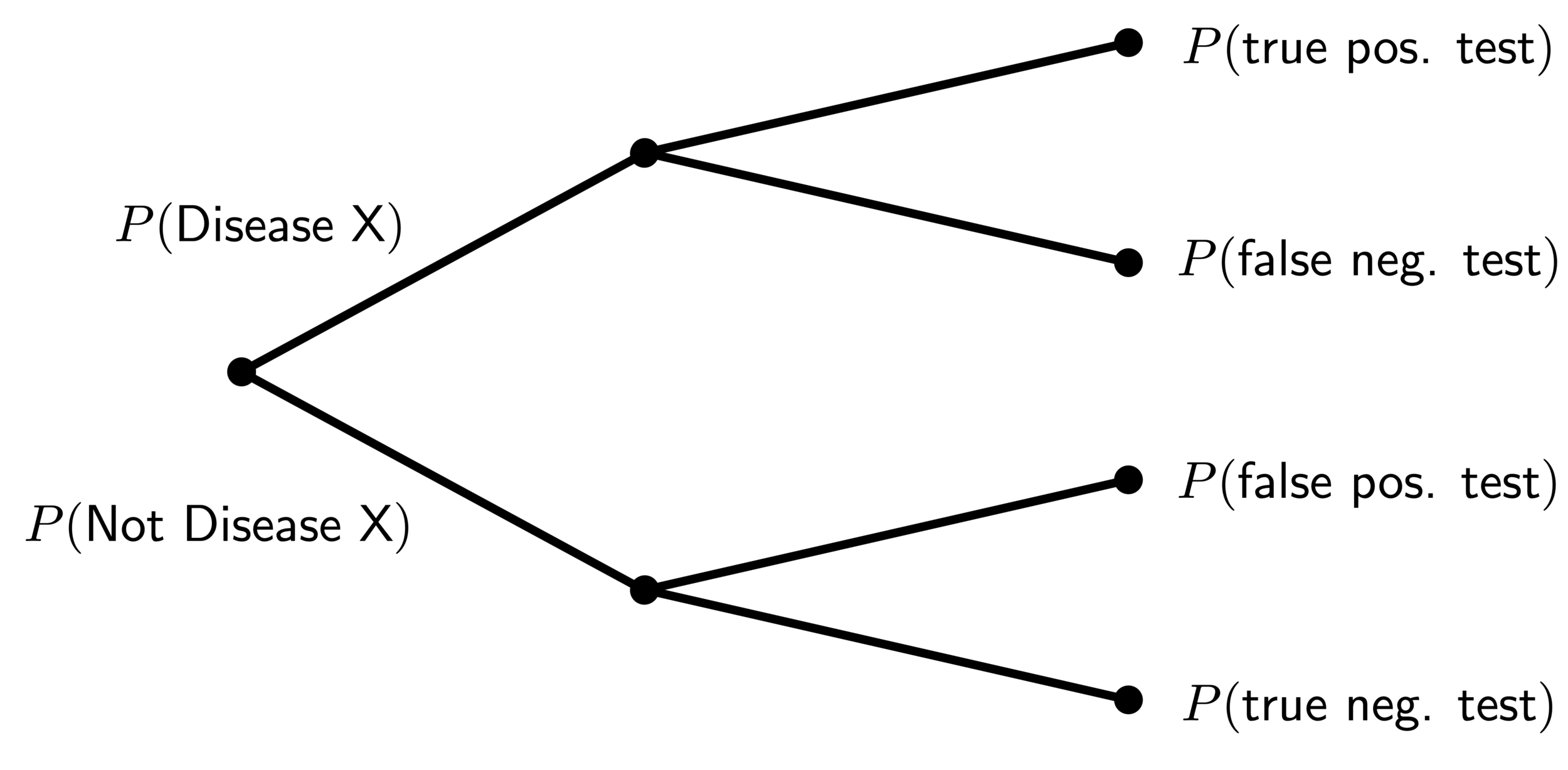
We know $P(\textsf{Disease X})$ outright, because we said the disease has a 1% prevalence, so that’s $.01$. We also know $P( \textsf{pos. test} | \textsf{Disease X})$, it’s $.99$ because we know the test has only a 1% false negative rate. To compute the overall probability of a positive test, it’s helpful to use this branching diagram:
The branching logic of computing conditional probability
To compute the probability of a positive test, we have to sum over all the possible ways we can get a positive test, and the probabilities of each. We follow both branches of having the disease or not, and then the probability of getting a positive test in each case. Putting this all together, we have that
$$P( \textsf{pos. test}) = \underbrace{P(\textsf{Not Disease X})}_{.99} \times \underbrace{P(\textsf{false positive})}_{.3} + \\ \underbrace{P(\textsf{Disease X})}_{.01} \times \underbrace{P(\textsf{true positive})}_{.99}$$
which gets us to $.3069$, the probability that any random person will get a positive result.
Putting all these into Bayes’ Theorem tells us that
$$P( \textsf{Disease X} | \textsf{pos. test} ) = \frac{\overbrace{P( \textsf{pos. test} | \textsf{Disease X})}^{.99} ~ \overbrace{P(\textsf{Disease X})}^{.01}}{\underbrace{P(\textsf{pos. test})}_{.01 \times .99 + .99 \times .3}} $$
which means that a single positive test would suggest about a 3.2% chance that you actually have the disease. This is driven by a relatively high false positive rate—if the false positive rate were 3%, then we would end up with a 25% probability that you have the disease. Still not high, but much, much higher than the 3.2% probability with our high false positive rate.
On the other hand, we may want to know the probability, given a negative test, that we’re actually ill, which is a much worse situation than a false positive. Specifically, we want to know
$$P( \textsf{Disease X} | \textsf{neg. test} ) = \frac{\overbrace{P( \textsf{neg. test} | \textsf{Disease X})}^{.01} ~ \overbrace{P(\textsf{Disease X})}^{.01}}{\underbrace{P(\textsf{neg. test})}_{.7 \times .99 + .01 \times .01}} $$
and we can recompute all of this using the same logic and find that a negative test leaves us with a .015% chance of actually having the disease, which is a result of having a test that produces very few false negatives and a disease that isn’t extremely prevalent. So we can rest easily if we get a negative test, but definitely want to follow up if we get a positive test.
A Second Opinion
We got our positive test, and the doctor wants to run the test again since we know our situation here. What happens to the probability of our having the disease if we then get a second test that comes back positive? The accuracy of the test remains unchanged, sure. But then we need to update some of our other priors. Specifically, $P(\textsf{Disease X})$ is 3.2% now, and we need to both $P(\textsf{pos. test})$ and recompute update $P(\textsf{Disease X})$.
We can trace the same calculation we did before, with the updated probability that we have this disease, given an existing positive test, becomes
$$P( \textsf{Disease X} | \textsf{neg.} ) = \frac{\overbrace{P(\textsf{pos.} | \textsf{Disease X})}^{.99} ~ \overbrace{P(\textsf{Disease X} )}^{.032}}{\underbrace{P(\textsf{pos.})}_{.032 \times .99 + .968 \times .3}} $$
Putting all this together gets us to about 9.8% chance of having the disease. Again, our high false positive rate kills our accuracy, and a test with the 3% false positive rate giving two positive results leads to a 92% chance of having Disease X.
What if we get good news in the second test, and it comes back negative? What’s the probability we actually have the disease? Well, that’s
$$P( \textsf{Disease X} | \textsf{neg.} ) = \frac{\overbrace{P( \textsf{neg.} | \textsf{Disease X})}^{.01} ~ \overbrace{P(\textsf{Disease X})}^{.032}}{\underbrace{P(\textsf{neg.})}_{.032 \times .01 + .968 \times .7}} $$
This leaves us with about a .048% chance that we’d have a positive test followed by a negative test if we actually had the disease. Intuitively, this should be the same as getting a negative test followed by a positive test, since the tests are independent, and indeed if we follow this logic, computing first $P(\textsf{Disease X} | \textsf{neg.})$ and using that to update our priors on the probability of having the disease, we get the same answer.
Final Thoughts
What’s interesting about Bayes’ Theorem not only tells us how to compute a probability, but also how to update our priors when new information becomes available. We saw what happens when we have successively more tests, and how updating our prior after each new test result changes our probabilities. We also saw that independent outcomes commute — we got the same probability having first a negative test then a positive test as we did having first a positive test then a negative test, which is a good check that we’re getting the right answer.
This will be a first entry in a series on using Bayes’ Theorem, as there’s a lot to explore with how to use it properly. In the next blog, I’ll go through both a rigorous and an intuitive derivation of Bayes’ Theorem, the later of which makes it easy to grasp what all these terms mean in terms of probabilities out of populations.